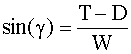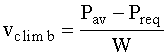Equations of Motion

climb situation

Let's look at the picture. In this picture, you see an autogyro in a steady climb. "Steady" means that it does not accelerate or slow down. As you see, the position angle of the autogyro is not the same as the angle of it's flight path (γ in the picture). This is often hard to imagine: aircraft climb less than we estimate them to, because we tend to confuse the position angle with the climb angle. Therefore, the propellor might have an angle-of-attack (α_T in the picture). In most flight types, this angle-of-attack is very small.
The total lift (L in the picture) only comes from the rotor. In reality, the fuselage might develop lift, but not enough to take that into account. Lift is defined to be always perpendicular to the flight path.
The total drag however (D in the picture), is generated by almost every part of the autogyro and is defined to be parallel to the flight path.
The weight is pointing down and is partly counteracting both lift and thrust.
We can now write down the equations of motion in the lift and in the drag direction:

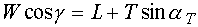	eq. 1
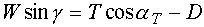	eq. 2

If the angle of incidence of the thrust can be neglected, these equations can be simplified to:

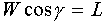	eq. 3
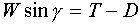	eq. 4

In horizontal flight, this can be further simplified to:

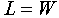	eq. 5
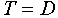	eq. 6

We can isolate γ in eq. 3 to obtain an equation for the clib performance:

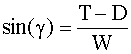eq. 7

climb speed

It is now wise to multiply the equation with the flying speed v. The left hand side of the equation then becomes the climb speed, while the forces on the right hand side become powers. (I hope you recall from physics class that a force multiplied with a speed becomes a power.)

eq. 8

All we have to do now is to substitute the right symbol for the terms: v_climb (climb velocity) for v*sin(γ), P_av (available power) for T*v and P_req (required power) for D*v.

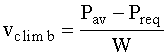eq. 9

The quantity P_av-P_req is also referred as the "power available for climb". If you want to see how the available and required power change with the flying speed, please take a look at the section "Flying behind the power curve" in the possible problems chapter.

From fixed-wing aircraft, the equation for the lift of the wing is known as:

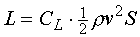eq. 10

In this formula, L is the total lift of the aircraft (per definition always perpendicular to the flying speed), ρ is the air density, v is the flying speed and S is the wing surface. C_L is a coëfficient that depends mainly on the shape and attitude of the aircraft. C_L is called coëfficient of Lift. This equation is also suitable for autogyros, except that autogyros do not have a wing surface. Instead, we will use the disc surface:

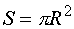eq. 11

It should be noted that we could also use the rotational speed of the rotor instead of the flying speed, because the lift depends on both of those speeds. However, rotorcraft pilots always try to keep the rotational speed at a constant value, so this dependency is "manually" removed. We can therefore say that the lift depends only on the flying speed. This is an approximation. Thus, for autogyros, the lift is given by:

eq. 12

The same formula is often derived using a dimension analysis (see appendix 2). In the same manner, the total drag of the aircraft is given by:

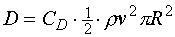eq. 13